Joint Seminar of the Department of Probability Theory & Vega Foundation

The schedule is subject to change

Language: Russian, English
Format: online

SCHEDULE FOR THE SPRING SEMESTER' 24 

April 10, 6:30-8:00pm (Moscow time)

 Vincent LIANG 
Melbourne University, Australia

On boundary crossing probabilities of diffusion processes

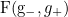We discuss two results related to the probability that a general time-inhomogeneous diffusion process 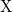stays between two curvilinear boundaries 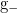and 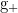(possibly with 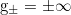) during a finite time interval.

First we discuss a discrete time discrete space Markov chain approximation to 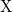with a Brownian bridge correction for computing 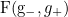. For a broad class of 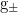and diffusion processes, we prove the convergence of the constructed approximations to 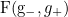in the form of products of the respective substochastic matrices as the time grid is getting finer. Numerical results indicate that the convergence rate is 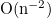in the case of 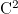-boundaries and a uniform time grid with steps.

In the second part of the talk, in the case when 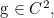we prove the existence of and obtain an explicit compact representation for the Gâteaux derivative 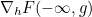of the boundary non-crossing probability functional in the direction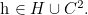

Joint work with K.\ Borovkov.

---

April 3, 6:30-8:00pm (Moscow time)

 Alexey METEYKIN 
postgraduate student of the Probability Theory Department, Moscow State University

Optimal market making using market order flow information

We consider the problem of optimal stochastic and impulse control for a market maker in an order book. The price is modeled by a doubly stochastic Poisson process with intensity depending on the market order flow. To solve the Hamilton–Jacobi–Bellman equation in the viscous sense, we construct a numerical scheme and investigate its convergence conditions.


 Arthur SIDORENKO 
postgraduate student of the Probability Theory Department, Moscow State University

The Meyer—Zheng Topology and Portfolio Investment with Proportional Transaction Costs

---

March 27, 6:30-8:00pm (Moscow time)

 Igor KOZIK 
dissertation candidate at the Department of Probability Theory (supervisor - V. Piterbarg)

Study and application of the connection between discrete and continuous time in modeling the trajectories of Gaussian processes taking into account high excursions

The report presents the exact asymptotics of the probabilities of exceeding an infinitely growing level on grids of various densities for Gaussian stationary processes, Gaussian nonstationary processes and Gaussian homogeneous fields in two-dimensional Euclidean space, the correlation functions of which behave at zero in a power-law manner for each of the coordinates, as the sampling step length decreases with level growth. The closeness of the obtained asymptotics to the corresponding ones in continuous time at different rates of grid condensation is discussed. Applications of the obtained results to the process of fractional Brownian motion and the problem of ruin of fractional Brownian motion and applications in terms of stochastization of the Hodgkin-Huxley model with modifications of Soto-Alexandrov are also given.

---

March 20, 6:30-8:00pm (Moscow time)

 Evgeniy PCHELINTSEV 
Head of the Laboratory of Statistics of Random Processes and Quantitative Financial Analysis, Tomsk State University

Efficient estimation of a regression function with small intensity L´evy noise

We consider the problem of nonparametric estimation in regression models with non-Gaussian Lévy noise under the condition that the unknown function belongs to the Sobolev ellipse.

Based on Pinsker's method, an exact lower bound is found for the normalized mean square accuracy of the estimates. For a Sobolev ellipse with exponential coefficients, the lower bound is calculated explicitly from complete and incomplete data.

---

March 13, 6:30-8:00pm (Moscow time)

 Jean JACOD 
Université Pierre & Marie Curie, Paris VI, France

Systematic Jump Risk

In a factor model for a large panel of N asset prices, a random time S is called a “systematic jump time” if it is not a jump time of any of the factors, but nevertheless is a jump time for a significant number of prices: one might for example think that those S’s are jump times of some hidden or unspecified factors. Our aim is to test whether such systematic jumps exist and, if they do, to estimate a suitably defined “aggregated measure” of their sizes. The setting is the usual high frequency setting with a finite time horizon T and observations of all prices and factors at the times iT/n for i = 0,...,n. We suppose that both n and N are large, and the asymptotic results (including feasible estimation of the above aggregate measure) are given when both go to ∞, without imposing restrictions on their relative size.

---

March 6, 6:30-8:00pm (Moscow time)

 Alexandra NOVIKOVA 
postgraduate student of the Probability Theory Department, Moscow State University

Skorokhod embedding problem. On its key solutions and applications

The purpose of this survey is to introduce the variety of aspects of the Skorokhod embedding problem: from initial formulation and motivation to further extensions and applications. Some prominent solutions, classified by the approaches for their construction, are going to be discussed. Each of them has distinctive properties which influence the further development of related theories and applications. In this regard, these properties are also under consideration.

---

February 28, 6:30-8:00pm (Moscow time)

 Elina AKHUNJANOVA 
6th year student of the Probability Theory Department, Moscow State University

Effects of intransitive interaction of customers on service characteristics in the M|M|1|2 system

We consider queuing systems with a Poisson input flow, one server and two waiting places in the queue. If the customer finds both places occupied, it will be rejected. In the basic system, when two customers are waiting in the queue, then each of them is selected for service with equal probability. Next, three types of customers are introduced with intransitive interaction according to the “rock-paper-scissors” game scheme (the types of customers are named accordingly for simplicity). Namely, if “rock” and “paper” are in the queue, then “paper” is selected, etc. It is assumed that customers of different types may arrive at different rates. We study what effects this interaction has on various characteristics of the system compared to the base system.


 Georgy MALINOVSKY 
postgraduate student of the Probability Theory Department, Moscow State University

Limit theorems for subcritical Bellman-Harris branching processes with long particle lifetimes and doubly stochastic Poisson immigration

Subcritical Bellman-Harris processes with long particle lifetimes and doubly stochastic Poisson immigration are considered. Particle lifetimes are assumed to have power-law tails with a index less than unity, leading to infinite average lifetimes. It is also assumed that the input stream of particle immigration has a random intensity, described by a stationary process with a correlation function limited by a decreasing power function. Under these conditions, the number of particles grows in a power-law manner (in contrast to the classical case with a finite average lifetime, when the number of particles has a limiting distribution). The law of large numbers and the central limit theorem are proven. An example with a stable distribution of lifetime is analyzed.

---

February 21, 6:30-8:00pm (Moscow time)

 Sergey ASEEV 
Corresponding member RAS, Head Department of Differential Equations Steklov Mathematical Institute

The Pontryagin maximum principle for infinite-horizon optimal control problems in economics

Infinite-horizon optimal control problems are commonly encountered in economic studies of growth processes. The infinite planning horizon introduces a singularity in such problems, leading to the emergence of various "pathological" phenomena in the relations of the maximum principle. In particular, the standard transversality conditions at infinity may not hold. We will present a recently developed comprehensive version of the Pontryagin maximum principle for the class of problems being considered. Additionally, we intend to discuss the economic interpretation of the maximum principle and provide an illustrative example.

---

SCHEDULE FOR THE FALL SEMESTER' 23 

November 29, 6:30-8:00pm (Moscow time)

 Mikhail URUSOV 
professor of the University of Duisburg-Essen, Germany

On certain stochastic control problems arising in optimal trade execution

We start with certain stochastic control problems where the control process acts as integrator both in the state dynamics and in the target functional. Problems of such type arise in the stream of literature on optimal trade execution pioneered by Obizhaeva and Wang (models with finite resilience).

We discuss how to extend the class of controls, first, from finite-variation processes to semimartingales and, second, beyond semimartingales. The need for such extensions arises when we introduce stochastically evolving liquidity parameters into the optimal trade execution problem.

The exposition covers some ideas from [1] and proceeds with [2].

This is a joint work with Julia Ackermann and Thomas Kruse.

References:

[1] Julia Ackermann, Thomas Kruse and Mikhail Urusov. Càdlàg semimartingale strategies for optimal trade execution in stochastic order book models. Finance and Stochastcis 25, 757-810, 2021. arXiv: https://arxiv.org/abs/2006.05863

[2] Julia Ackermann, Thomas Kruse and Mikhail Urusov. Reducing Obizhaeva-Wang type trade execution problems to LQ stochastic control problems. Accepted in Finance and Stochastics, 2023. arXiv: https://arxiv.org/abs/2206.03772

---

November 22, 6:30-8:00pm (Moscow time)

 Marina MIKITCHUK 
Postgraduate student, Moscow School of Economics, Moscow State University; scholarship holder of Vega Institute Foundation

Development assistance: the effectiveness of the benefit-oriented motive and its formation factors

Official development assistance is one of the central mechanisms for overcoming cross-country inequality. Its volumes are constantly increasing and at present surpass US$180 billion. The task of effective aid allocation remains relevant and has no trivial solution. The report presents an econometric analysis of the effectiveness of transfers, taking into account the motivation of donors. In addition, conclusions about the conditions for the formation of disinterested assistance are proposed for discussion.

---

November 15, 6:30-8:00pm (Moscow time)

 Dean FANTAZZINI 
Doctor of Economics, Professor of the Department of Econometrics and Mathematical Methods of Economics, Moscow School of Economics, Moscow State University

Detecting Pump-and-Dumps with Crypto-Assets: Dealing with Imbalanced Datasets and Insiders’ Anticipated Purchases

Detecting pump-and-dump schemes involving cryptoassets with high-frequency data is challenging due to imbalanced datasets and the early occurrence of unusual trading volumes. To address these issues, we propose constructing synthetic balanced datasets using resampling methods and flagging a pump-and-dump from the moment of public announcement up to 60 min beforehand. We validated our proposals using data from Pumpolymp and the CryptoCurrency eXchange Trading Library to identify 351 pump signals relative to the Binance crypto exchange in 2021 and 2022. We found that the most effective approach was using the original imbalanced dataset with pump-and-dumps flagged 60 min in advance, together with a random forest model with data segmented into 30-s chunks and regressors computed with a moving window of 1 h. Our analysis revealed that a better balance between sensitivity and specificity could be achieved by simply selecting an appropriate probability threshold, such as setting the threshold close to the observed prevalence in the original dataset. Resampling methods were useful in some cases, but threshold-independent measures were not affected. Moreover, detecting pump-and-dumps in real-time involves high-dimensional data, and the use of resampling methods to build synthetic datasets can be time-consuming, making them less practical.

---

November 8, 6:30-8:00pm (Moscow time)

 Vladimir KUTSENKO 
postgraduate student of the Probability Theory Department, Moscow State University

Simulation of branching random walks in a random environment

The talk is devoted to branching random walks (BRW) on a multidimensional lattice with continuous time in a random environment. The BRW describes a system of particles that can walk on the lattice, split and disappear independently of each other. In the model under consideration, the process starts with a single particle at an arbitrary point on the lattice. The laws of particle multiplication and death are realized randomly before the process starts. The talk will present the main theoretical results obtained for some models of BRW in a random environment. However, the main attention will be given to the description of numerical methods that have been used to investigate theoretically predicted effects at finite times, for example, the "intermittency" effect.

---

November 1, 6:30-8:00pm (Moscow time)

 Ekaterina PALAMARCHUK 
Cand. sc. in Mathematics and Physics, CEMI RAS, NRU HSE, MI RAS)

Study on linear stochastic control systems under non-ergodic optimality criteria

The report examines linear stochastic time-varying systems. Such systems can be related to models from numerous fields of applications, including economics and finance. We investigate and assess long-term risks by considering integral quadratic performance indices and solving infinite-time control problems. Several examples of linear control systems are also provided, including cases of time-varying diffusion matrix, various discounting types in the performance index, as well as stochastic time-scales.

---

October 25, 6:30-8:00pm (Moscow time)

 Platon PROMYSLOV 
Postgraduate student, Department of Probability Theory, Moscow State University; scholarship holder of Vega Institute Foundation

Ruin probabilities for a Sparre Andersen model with investments: the case of annuity payments

In recent studies, the Sparre Andersen insurance company model has been enriched by the assumption that the insurance company's capital reserve is fully invested in a risky asset. In this model, for the case of non–life insurance, with fairly moderate hypotheses, the asymptotic behavior is essentially the same as for generalizations of the Kramer-Lundberg model. The report will consider the Sparre Anderson model in the case when the price of a risky asset is set by a geometric Levy process, and jumps in the business process are positive.

---

October 18, 6:30-8:00pm (Moscow time)

 Oleg KUDRYAVTSEV 
Doctor of Physical and Mathematical Sciences, Associate Professor

Modern problems of computational financial mathematics

---

You can watch the meetings that took place earlier in the playlist of the Foundation's channel. 

BACK TO THE COURSE LIST